Be Dynamic
As we have seen, the Flow model keeps data on the master and each time it is needed it is sent to all workers regardless of what data was there before. When a lot of data is sent to workers, there is an increase in overhead and a decrease in performance. In this case, it can be reasonable to use the dynamic model. This model is very similar to the flow model, but it is a SPMD program. The difference is that data is kept on all processors so it is ready for use. This condition requires that after a parallel part of code is executed each node sends new data to all the other nodes. The other main feature of this model is that all processors execute the same code until they need I/O or need to execute a parallel section. I/O is executed only on first (master) node. Parallel sections are executed similar to the flow model. The sidebar shows an example of the dynamic algorithm.
| Sidebar: A Dynamic Algorithm |
IF(master) THEN
n_parts = n_workers = m+2 ! compute number of
! parallel parts
DO i_part=1, n_workets
receive data from worker w
load_worker(w) ! send to worker next
! portion or end signal
ENDDO
ELSE
work = .true.
DOWHILE(work)
compute (first time) or receive next part
goto (1, 2, 3, 4), part
1 receive x from master
call s1(x) ! first part (block)
send x to master
goto 5
2 receive imin, imax, y(imin:imax) from master
DO i = imin, imax
call s2(y(i))
ENDDO
send y(imin:imax) to master
goto 5
3 receive z from master
call s3(z) ! first part (block)
send z to master
goto 5
4 work = .false. ! end of work
5 CONTINUE
ENDDO
ENDIF
broadcast(x, y, z) ! broadcast from master to all
|
The load balance of the dynamic algorithm is practically the same as with the flow model. Which model is best to use? The answer depends on how much data is used and how much data is produced by the parallel segments.
The Static Model
One may notice that the local memory of a node is used not very efficiently in the previous models. When large amount of data are used it can be desirable to keep only part of data on each node to minimize data movement and to support large problems.The static model is based on array distribution and is probably the most common model used for parallelization. This strategy means that arrays are split between computational nodes, and operations are performed on these elements on specific nodes. For example the following code fragment can be executed with a static model.
REAL Y(N) ... DO I = 1, N CALL S2(Y(I)) ENDDO
A static parallelization is shown in the sidebar.
| Sidebar: Example static parallelization |
! suppose that n is divisible by n_nodes real y(n/n_nodes) ... low = P*(n/N_nodes)+1 if(current_node .eq. node1) then s1(x) else if(current_node .eq. node2) then s3(z) endif high = (P+1)*(n/N_nodes) do I = low, high call s2(y(I- P*(n/N_nodes)) enddo
|
In general, as the number of nodes increases, the amount of memory needed per node decreases because smaller portions of the array are placed on each node. Let's look again at the program. With a static parallelization we can assign S1 to Node 1 and S3 to Node 3 as before. We will then distribute array Y on all four nodes. Figure Four shows this distribution.
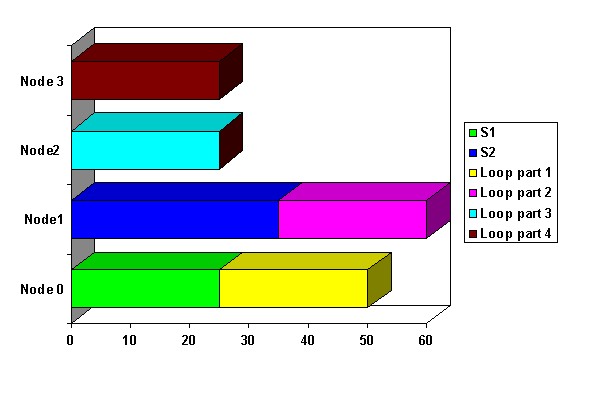
We get 60 ms again. Can we do better? Another way is to distribute the array is on a subset of nodes, in this case two nodes. Then for the same program we can get the following diagram.
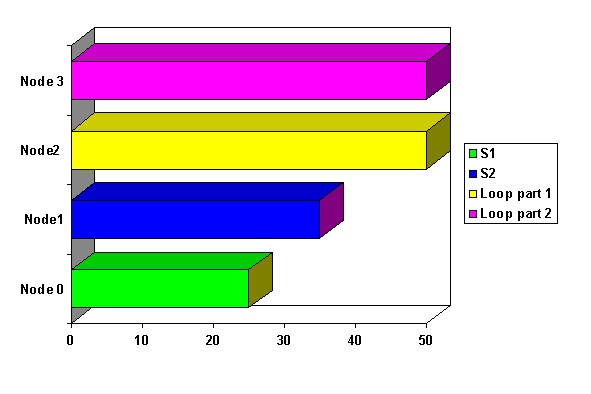
Now we got 50 ms for the program. This result is a good, but the price one has paid for this model is that the balancing of parallel loops is more "rigid" than you may like.
A Recap
At this point, a summary may help to understand the differences between the models. In the Flow model, programs are executed as MPMD and there is no data partitioning. The master node basically acts as a distributor and collector of data. The worker nodes are sent data which is processed and sent back to the master node. The scheduling is dynamic which means that it can accommodate variations in run-times and still maintain a good efficiency. (i.e. Run-time decisions can be made as to whether a certain loop should be executed in parallel) The size of the program and data is limited by the size of the master node.The Dynamic model programs are executed as SPMD and like the Flow model there is no partitioning. Each node, including the master, has the same program. All nodes are kept up to date at the completion of each parallel part of the program. The scheduling is dynamic and the size of the problem is limited by the size of a node because the entire program and data must fit on each node.
The Static model is SPMD as well, however, the data is partitioned across nodes. The scheduling is static and thus could have lower efficiencies if loop boundaries change from run to run. (i.e. The program is committed to parallel execution at certain points in the program) The size of the program can be very large as the data are sliced and placed on different nodes.
This article was originally published in ClusterWorld Magazine. It has been updated and formatted for the web. If you want to read more about HPC clusters and Linux, you may wish to visit Linux Magazine.
Pavel Telegin is currently Department Head of Programming Technology and Methods in the Joint Supercomputer Center, Moscow, Russia.


